Demo-PY5: Machine Learning mit Keras und Tensorflow:
Prognose von Stromverbrauchsdaten
Das elab2go-Tutorial Demo-PY5 zeigt die Erstellung eines Künstlichen Neuronalen Netzwerks für eine Regressionsaufgabe mit Hilfe der Machine Learning-Frameworks Keras und Tensorflow. Als Datenbasis wird ein aggregierter OPSD-Datensatz zum Stromverbrauch in Deutschland verwendet. Es wird ein Deep Learning-Modell mit mehreren Long Short-Term Memory (LSTM)-Schichten trainiert, validiert und damit eine Prognose über die zukünftige Entwicklung der Stromverbrauchsdaten erstellt. Die Daten werden in der interaktiven, webbasierten Anwendungsumgebung Jupyter Notebook analysiert.
Motivation
Machine Learning befasst sich mit der Entwicklung lernfähiger Systeme und Algorithmen, und verwendet dabei Konzepte und Methoden der Statistik und der Informationstheorie. In den letzten Jahren haben Künstliche Neuronale Netze und insbesondere Deep Learning die Forschung beflügelt, insbesondere deren Anwendungen im Bereich der Bild- und Sprachverarbeitung.
Eine weiteres Anwendungsgebiet ist der Einsatz neuronaler Netzwerke in der Zeitreihenprognose. Im Vergleich zu zu statistischen AR-Prognosemodellen wie ARIMA (AutoRegressive-Moving Average)-Modellen haben Künstliche Neuronale Netze den Vorteil, dass sie akzeptable Prognose-Ergebnisse liefern, auch ohne alle statistischen Parameter der Zeitreihe ermitteln zu müssen. Voraussetzung ist das Vorhandensein von ausreichend Vergangenheitsdaten und einige Geduld bei der Erstellung und beim Trainieren des Netzwerks.
Zur Prognose einer Zeitreihe legt man ein gleitendes Zeitfenster mit n Werten der Vergangenheit über die Zeitreihe. Die Trainingsaufgabe besteht darin, aus den bekannten Werten deren Zukunft zu schätzen, d.h. aus n Werten in der Eingabe-Schicht auf den nächsten Wert zu schließen.
Warum Künstliche Neuronale Netzwerke?
Künstliche Neuronale Netze sind Machine Learning-Modelle, die den neuronalen Prozessen des Gehirns nachempfunden sind und für Klassifikations-, Prognose- und Optimierungsaufgaben verwendet werden. Künstliche Neuronale Netzwerke sind geeignet, um komplexe und nichtlineare Zusammenhänge in Daten zu lernen. Sie sind gut skalierbar und können auch für große Datensätze eingesetzt werden.
Warum Keras und Tensorflow?
Das aktuell meistgenutzte Framework für die Entwicklung von Künstlichen Neuronalen Netzwerken und Deep-Learning-Modellen mit Python ist Keras mit Tensorflow als Backend. Tensorflow ist ein von Google entwickeltes Framework für maschinelles Lernen, das Open-Source mit MIT-Lizenz verfügbar ist. Keras ist eine Open-Source-Python- Bibliothek zum Entwickeln und Bewerten von Machine Learning-Modellen, das als benutzerfreundliche Schnittstelle zum Tensorflow-Framework verwendet wird.
Übersicht
Demo-PY5 ist in zehn Abschnitte gegliedert. Zunächst wird der OPSD-Datensatz beschrieben und die Fragestellung erläutert, die wir mit unserer Datenanalyse beantworten wollen. Im nächsten Abschnitt werden grundlegende Konzepte Künstlicher Neuronaler Netzwerke vorgestellt. Danach wird die Erstellung des Jupyter Notebooks und Verwendung der benötigten Bibliotheken erläutert. Anschließend erfolgt die Umsetzung, die dem Lebenszyklus des Überwachten Lernens folgt, die Datenvorbereitung (Aufteilung in Trainings- und Testdaten, Normierung, Festlegen der Zielvariablen), die Definition des Modells, das Trainieren und Validieren des Modells, und schließlich seine Verwendung für die Prognose (vgl. Abbildung).
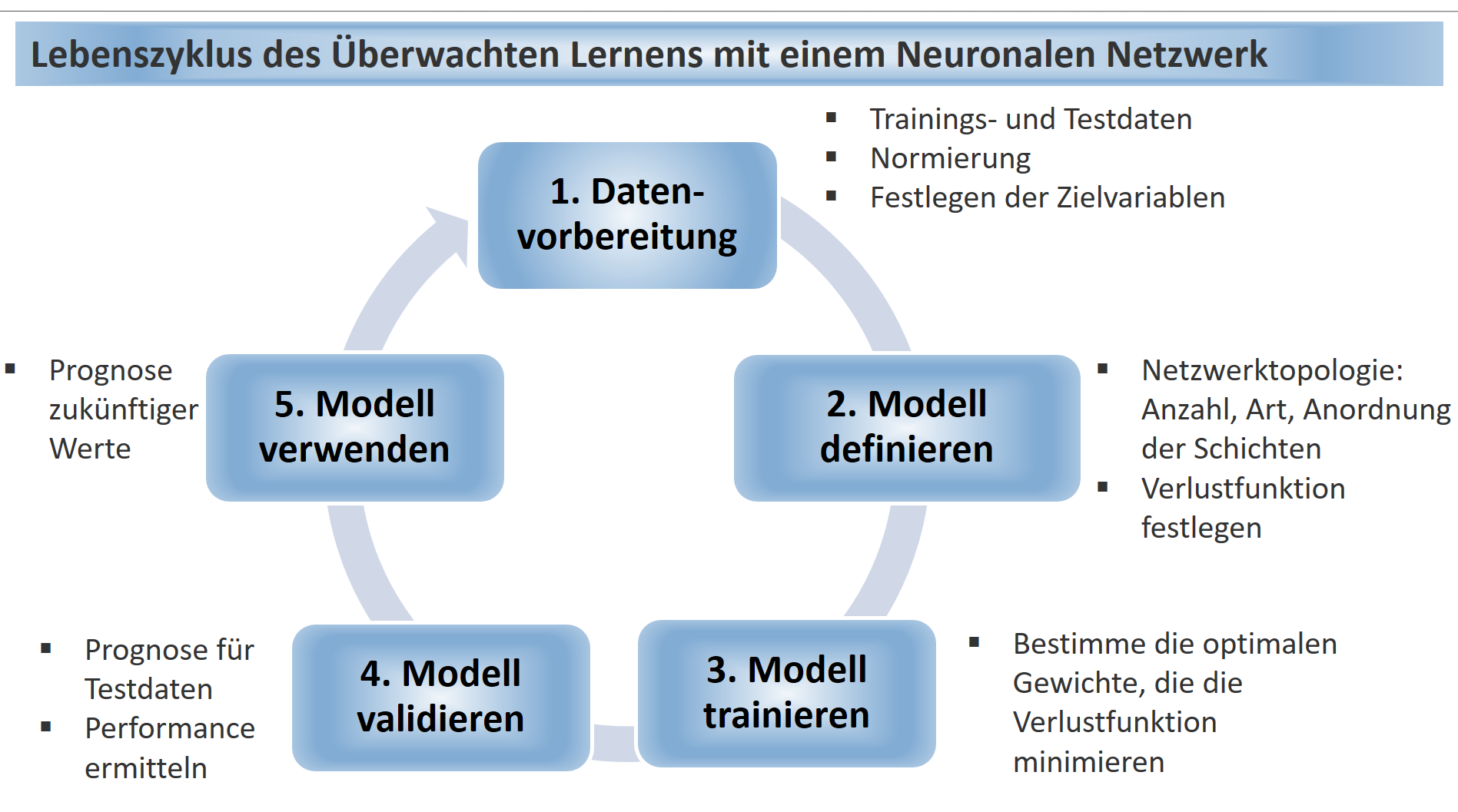
6 Datenvorbereitung: 6-1 Daten einlesen, 6-2 Stationarität, 6-3 Aufteilung in Trainings- und Testdaten, 6-4 Skalierung der Daten, 6-5 Festlegen der Merkmale und Zielvariablen
7 Modell erstellen und trainieren: 7-1 Modell erstellen, 7-2 Modell trainieren
8 Modell validieren: 8-1 Prognose für Validierungsdaten, 8-2 Performance der Validierung ermitteln
1 Der Stromverbrauch-Datensatz
Open Power System Data ist eine offene Plattform für Energieforscher, die europaweit gesammelte Energiedaten in Form von csv-Dateien und sqlite-Datenbanken zur Verfügung stellt. Die Daten können kostenlos heruntergeladen und genutzt werden. Die Plattform wird von einem Konsortium der Europa-Universität Flensburg, TU Berlin, DIW Berlin und Neon Neue Energieökonomik betrieben, mit dem Ziel, die Energieforschung zu unterstützen. Die Stromverbrauch-Rohdaten werden auf der OPSD-Plattform unter dem Menüpunkt Time Series zum Download angeboten, in unterschiedlichen Formaten und Auflösungen: time_series.xlsx, time_series_15min_singleindex.csv, time_series_30min_singleindex.csv, time_series_60min_singleindex.csv.
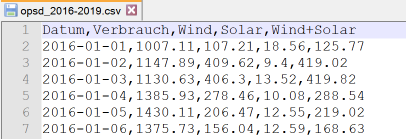
Für Demo-PY5 verwenden wir als Datenbasis einen aggregierten OPSD-Zeitreihen-Datensatz zum Stromverbrauch in Deutschland, der den Datenzeitraum: 01.01.2016 - 31.12.2019 mit einer täglichen Auflösung abbildet. Die csv-Datei mit den Spalten Datum, Verbrauch, Wind, Solar, Wind+Solar enthält insgesamt 1461 Zeilen. Wie in Demo-PY2: Aufbereitung des OPSD-Datensatzes beschrieben, wird die Datei mit den Rohdaten time_series_60min.csv in ein DataFrame eingelesen, die relevanten Spalten werden extrahiert, und die Zeitskala wird durch ein Resampling geändert, so dass Daten mit täglicher Auflösung erhalten und in eine neue CSV-Datei mit dem Namen opsd_2016-2019.csv exportiert werden können.
2 Die Fragestellung
Ziel ist, auf Basis der Vergangenheitsdaten für die Jahre 2016 bis 2019 den Stromverbrauch für 2020 vorherzusagen und die Performance der Prognose zu ermitteln.Da das Jahr 2020 inzwischen auch schon in der Vergangenheit liegt, können wir die vorhandenen tatsächlichen Daten für einen Vergleich heranziehen. Dafür wird zunächst als Vorhersagemodell ein Künstlichen Neuronalen Netz erstellt. Entsprechend der Vorhergehensweise des überwachten Lernens wird der Datensatz in Trainings- und Testdaten aufgeteilt, das Modell wird mit Hilfe der Trainingsdaten trainiert und mit Hilfe der Testdaten validiert. Als Performancemaß für die Güte der Prognose verwenden wir die mittlere quadratische Abweichung bzw. mittlere Fehlerquadratsumme (engl. Mean Square Error, MSE) bzw. die Wurzel der mittleren Fehlerquadratsumme (engl. Root Mean Square Error, RMSE), diese Maße werden in der Statistik üblicherweise eingesetzt, um die Güte einer Schätzung zu bewerten.
3 Was ist ein Neuronales Netz?
Künstliche Neuronale Netze sind Machine Learning-Modelle, die den neuronalen Prozessen des Gehirns nachempfunden sind und für Klassifikations-, Prognose- und Optimierungsaufgaben verwendet werden. Ein Künstliches Neuronales Netz besteht aus Neuronen, d.h. Knoten bzw. Verarbeitungseinheiten, die durch gerichtete und gewichtete Kanten verbunden und in Schichten angeordnet sind (Eingabeschicht, versteckte Schichten und Ausgabeschicht). Eine Kante von Neuron i zu Neuron j hat das Gewicht wi,j, die die Stärke der Verbindung zwischen den Neuronen angibt. Die Eingabedaten werden innerhalb des Netzes von den Neuronen über Aktivierungsfunktionen verarbeitet und das Ergebnis wird bei Überschreiten eines Schwellwertes an die Neuronen der nächsten Schicht weitergegeben.
| Neuron: | Funktionsweise: |
|---|---|
|
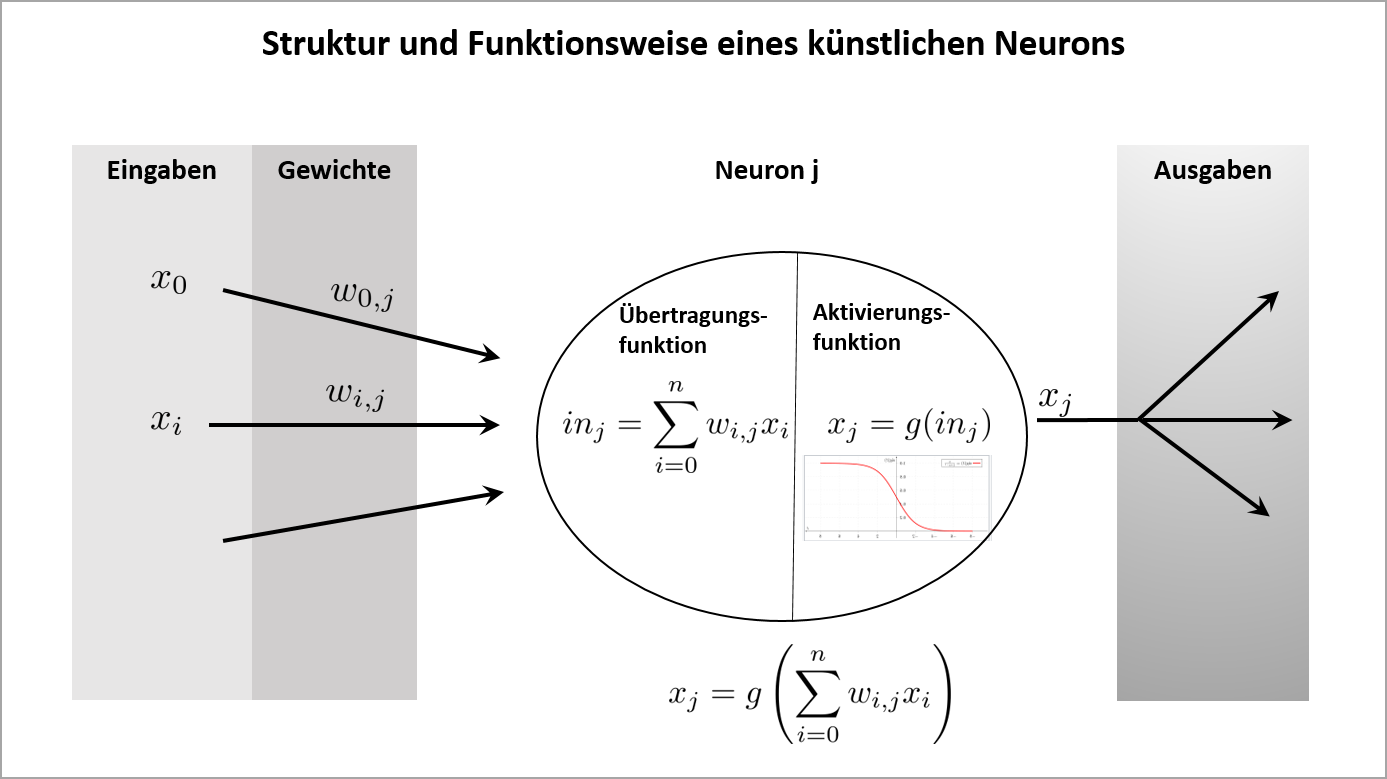
Das vereinfachte Modell eines künstlichen Neurons nach McCulloch und Pitts (1943) besteht aus einer Verarbeitungseinheit mit gewichteten Eingaben und einer Ausgabe, die durch das Zusammenschalten zweier Funktionen (Übertragungsfunktion und Aktivierungsfunktion) berechnet wird. Ein Neuron j berechnet mit Hilfe der Übertragungsfunktion zunächst die gewichtete Summe seiner Eingaben und wendet darauf die Aktivierungsfunktion an, um seine Ausgabe zu berechnen. Falls die Ausgabe einen festgelegten Schwellwert überschreitet, wird sie an die Neuronen der nächsten Schicht propagiert. |
Die Aktivierungsfunktion ist eine monoton steigende und differenzierbare Funktion, die (stückweise) linear oder nichtlinear sein kann. Nichtlineare Aktivierungsfunktionen haben den Vorteil, dass mit ihrer Hilfe nichtlineare Abhängigkeiten zwischen den Ein- und Ausgaben des Neuronalen Netzwerks erlernt werden können. Häufig verwendete Aktivierungsfunktionen sind die sigmoid-, die tanh- und die relu- Funktion. Wegen dem Problem des verschwindenen Gradienten können sigmoid und tanh für Netzwerke mit vielen Schichten schlecht eingesetzt werden. In diesem Fall sind stückweise lineare Aktivierungsfunktionen wie die relu-Funktion das Mittel der Wahl.
Die Trainingsphase eines neuronalen Netzwerkes besteht darin, die Gewichte zu erlernen, die zu den vorgegebenen Trainingsdaten passen. Der Trainings-Algorithmus wird auf die Lösung eines Optimierungsproblems zurückgeführt, bei dem das Minimum der Kostenfunktion (des Fehlers der Ausgabeschicht) bestimmt werden muss. Da die einzelnen Aktivierungsfunktionen, die in die Bildung der Kostenfunktion eingehen, differenzierbar sind, kann das Optimierungsproblem mit Gradientenabstiegsverfahren gelöst werden.
Abhängig von der Topologie der Neuronalen Netze (d.h. Anordnung der Schichten) unterscheidet man
- Feedforward-Netze, bei denen die Weiterleitung nur in eine Richtung von der Eingabe- zur Ausgabeschicht erfolgt,
- Rekurrente Netze, die Verbindungen von Neuronen einer Schicht zu Neuronen derselben oder einer vorangegangenen Schicht haben. Durch die rückgekoppelten Verbindungen erhält das Netz ein Gedächtnis.
- Long Short Term Memory-Netze (LSTM), eine Verbesserung rekurrenter Netze, bei denen die Neuronen einen komplexeren Aufbau haben und einen konfigurierbaren Anteil der Ausgaben auch wieder vergessen können.
4 Jupyter Notebook erstellen
Wir verwenden die Programmiersprache Python, sowie die Entwicklungs- und Paketverwaltungsplattformen Anaconda, Spyder und Jupyter Notebook, die umfangreiche Funktionalität für Paketverwaltung, Softwareentwicklung und Präsentation bereitstellen. Das Neuronale Netzwerk wurde zunächst mit der Entwicklungsumgebung Spyder entwickelt, was den Vorteil hat, dass man die Werte der Variablen im Workspace einsehen kann und auch eine Debugging-Funktionalität zur Verfügung hat, dies erleichtert die Fehlersuche. Das funktionierende Modell wurde danach auch als Jupyter Notebook erstellt und mit Markdown-Erläuterungen versehen. Die Details der Verwendung von Anaconda und Jupyter Notebook sind in Demo-PY1 Installation von Python und Anaconda und Jupyter Notebook verwenden beschrieben.
Für die Datenvorbereitung und Erstellung des Prognosemodells wird ein Jupyter Notebook erstellt.
In Anaconda wird zunächst eine neue Umgebung (engl. Environment) mit dem Namen KNN-Demos angelegt, in die die benötigten Programmpakete
installiert werden: keras, tensorflow, scikit-learn, matplotlib, seaborn, graphviz, pydot.
Die Installation erfolgt über die Anaconda-Befehlskonsole mit Hilfe der Paketverwaltungsprogramme pip oder conda:
mit Hilfe des Befehls pip install keras wird z.B. das Programmpaket keras installiert,
mit Hilfe des Befehls pip install tensorflow das Paket tensorflow, etc.
In dem angewählten Environment KNN-Demos wird dann die Jupyter Notebook-Anwendung geöffnet und mit Hilfe des Menüpunkts "New" ein neues Python3-Notizbuch mit dem Namen elab2go-Demo-PY5 angelegt.
5 Bibliotheken importieren
In Python kann man mit Hilfe der import-Anweisung entweder eine komplette Programmbibliothek importieren, oder nur einzelne Funktionen der Programmbibliothek (from-import-Anweisung). Beim Import werden für die jeweiligen Bibliotheken oder Funktionen Alias-Namen vergeben: für numpy vergeben wird den Alias np, für pandas vergeben wir den Alias pd.
Die Bibliotheken müssen vor Verwendung installiert sein. Falls Anaconda verwendet wird, kann die erfolgreiche Installation überprüft werden, indem in der Liste der installierten Pakete (engl. packages) nach keras, tensorflow etc. gesucht wird.
In der ersten Codezelle des Jupyter Notebook importieren wir die benötigten Programmbibliotheken: numpy, pandas, sklearn, keras und matplotlib, sowie Funktionen und Klassen aus diesen Bibliotheken. Hier werden nur die mehrfach benötigten Pakete angeführt. Pakete, die nur in einer einzigen Codezelle benötigt werden, kann man auch dort importieren. numpy wird für die Speicherung der Daten in Arrays und nützliche Funktionen benötigt, pandas für die Datenaufbereitung, keras für die Erzeugung und Verwendung der Neuronalen Netzwerke. Das sklearn-Packet metrics enthält Funktionen, mit denen man die Güte eines Vorhersagemodells bewerten kann.
Codezelle 1: Programmbibliotheken importierenimport numpy as npimport pandas as pdfrom datetime import datetimeimport math# matplotlib und seaborn für Grafikenimport matplotlib.pyplot as pltimport seaborn as sns# sklearn für Überwachtes Lernenfrom sklearn.preprocessing import MinMaxScalerfrom sklearn.metrics import mean_squared_errorfrom sklearn.metrics import max_error# keras für Neuronale Netzeimport keras as kerasfrom keras.models import Sequentialfrom keras.layers import Dense, LSTM, Dropoutfrom keras.utils import plot_model# Für das Darstellen von Bildern im SVG-Formatimport graphviz as gvimport pydotfrom keras.utils import model_to_dotfrom IPython.display import SVG
6 Datenvorbereitung
Die Datenvorbereitung im Rahmen des Machine Learning besteht darin, die externe Datenquelle in eine Form zu bringen, die von dem modellbildenden Verfahren erwartet wird. Dazu gehören folgende Schritte:
- 6-1 Einlesen und Visualisierung der Daten, inklusive Datenbereinigung. In Python werden der Daten im Arbeitsspeicher des Programms als DataFrames oder NumPy Arrays gespeichert, dabei muss auch öfters zwischen den unterschiedlichen Darstellungen konvertiert werden.
- 6-2 Untersuchen der statistischen Eigenschaften der Daten. Im Falle einer Zeitreihe ist es die Stationarität.
- 6-3 Aufteilen der Datenquelle in Trainingsdaten und Testdaten. Dieser Schritt ist stets dann erforderlich, wenn wir ein Modell des überwachten Lernens implementieren.
- 6-4 Skalieren der Daten (Standardisieren, Normalisieren etc.). Dieser Schritt ist in Neuronalen Netzwerken erforderlich, damit die Daten alle dieselbe Größenordnung haben.
6-1 Daten einlesen und visualisieren
Der OPSD-Datensatz, der in Form einer komma-getrennten csv-Datei opsd_2016-2019.csv vorliegt, wird zunächst mit Hilfe der Pandas-Datenstrukturen und Funktionen eingelesen, aufbereitet und tabellarisch ausgegeben und visualisiert.
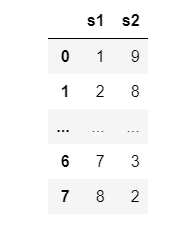
Für die Visualisierung von Pandas-DataFrames definieren wir eine Hilfsfunktion mit dem Namen display_dataframe(), die ein DataFrame mit der angegebenen maximalen Anzahl an Zeilen und Spalten formatiert ausgibt. Wir testen die Funktion, indem wir ein DataFrame df mit zwei Spalten und acht Zeilen erstellen und davon jedoch nur 4 Zeilen ausgeben. Die Ausgabe ist wie abgebildet: die ersten und letzten beiden Zeilen werden ausgegeben, die anderen durch Punkte angedeutet.
| Code-Zelle 2: Hilfsfunktion display_dataframe | Ausgabe: |
|---|---|
|
 |
Danach werden die Daten mit Hilfe der Funktion read_csv() in einen DataFrame mit dem Namen opsd_df eingelesen und die Spalte Verbrauch (unsere Rohdaten für die Zeitreihe) wird in einen DataFrame series extrahiert.
- Zeile 2: Die Datum-Spalte wird als Index des DataFrames festgelegt.
- Zeile 4: Fehlende Werte, die im DataFrame als NaN (Not Available) angezeigt werden, ersetzen wir mit Hilfe der Funktion fillna durch den jeweils vorigen Wert der Zeitreihe.
- Zeile 6: Die Zahlenwerte werden auf zwei Nachkommastellen gerundet.
- Zeile 8: Ausgabe des DataFrames mit Hilfe der Funktion display_dataframe()
Die Ausgabe der ersten und letzten 3 Zeilen des DataFrames sieht wie rechts abgebildet aus. Wir definieren in diesem Codeblock noch zwei Variablen für die spätere Verwendung: series bezeichnet die Spalte / Zeitreihe (engl. series), für die wir die Prognose erstellen wollen. anzZ bezeichnet die Anzahl Zeilen des DataFrames, die wir mit Hilfe der Funktion shape herausfinden.
| Code-Zelle 3: Daten einlesen | Ausgabe: |
|---|---|
|
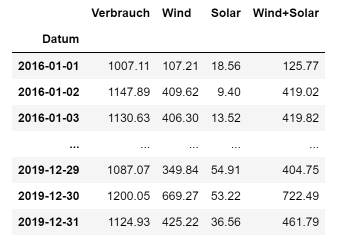 |
Die Visualisierung der Daten der Verbrauchsspalte zeigt, dass die Daten über die Jahre 2016 bis 2019 saisonale Peaks um Jahresmitte und Jahreswende und einen geringen Trend aufweisen. Wir erzeugen die grafische Darstellung hier mit Hilfe der Grafik-Funktionen der pandas-Bibliothek.
Codezelle 4: Visualisierung der VerbrauchsdatenAusgabe:sns.set(rc={'figure.figsize':(12, 4)})sns.set_color_codes('bright')ax = series.plot(linewidth=1, color='b')ax.set_title('Täglicher Stromverbrauch')ax.set_xlabel('Datum');ax.set_ylabel('GwH');
6-2 Stationarität untersuchen
Eine stationäre Zeitreihe hat zu allen Zeitpunkten den gleichen Erwartungswert und die gleiche Varianz. Stationarität ist eine wünschenswerte Eigenschaft, um ein funktionierendes Prognosemodell erstellen zu können. Falls eine Zeitreihe z.B. einen starken Trend oder Saisonalitäten hat und komplett unterschiedliches Verhalten über die Zeit hinweg hat, ist die Erstellung einer Prognose schwieriger. Zeitreihen könnnen durch diverse mathematische Transformationen stationär gemacht werden.
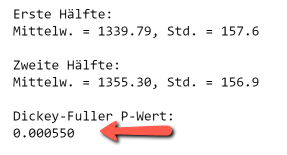
In diesem Vorbereitungsschritt wird die Zeitreihe auf Stationarität untersucht, zunächst empirisch, dann mit Hilfe des Dickey-Fuller-Tests. Stichprobenartige Auswertungen des Erwartungswertes und der Varianz für die Verbrauchsdaten ergeben ähnliche Werte für verschiedene Bereiche der Zeitreihe. Der Dickey-Fuller Test bestätigt diese Erkenntnis: der p-Wert, der aus der Anwendung der Funktion adfuller erhalten wird, ist kleiner als 0.05, und damit ist die Hypothese, dass die Zeitreihe nicht stationär ist, widerlegt.
| Code-Zelle 5: Stationarität | Ausgabe: Mittelw., Stdabw., p-Wert |
|---|---|
|
 |
Eine Zeitreihe, die Trends und Saisonalitäten aufweist, kann durch mathematische Umformungen in eine gleichwertige stationäre Zeitreihe umgewandelt werden. Falls z.B. ein jährlicher Peak um die Jahreswende auffällt, kann durch Differenzenbildung (von jedem Tageswert eines Jahres wird der Wert des Vorjahres abgezogen) eine neue Zeitreihe erstellt werden, die diese Saisonalität nicht aufweist. Die Prognose würde dann für die stationäre Zeitreihe durchgeführt werden. Da diese mathematischen Transformationen jedoch zusätzliche Komplexität einführen und unser Fokus hier die Erstellung des Neuronalen Netzwerkes ist, erstellen wir unser Prognosemodell auf der vorhandenen Zeitreihe und verzichten zunächst auf eine Transformation.
Die weitere Datenvorbereitung besteht darin, die aus der CSV-Datei importierten Rohdaten in eine Form zu bringen, die die Keras-Funktionen für die Erstellung eines Neuronalen Netzes als Eingabedaten akzeptieren. Da die Prognose nur für die Stromverbrauchsdaten (d.h. erste Spalte des Datensatzes) erfolgen soll, sind das unsere Rohdaten. Diese müssen in Trainings- und Testdaten aufgeteilt, auf den Wertebereich (0, 1) skaliert, und in ein Überwachtes-Lernen-Problem überführt werden, indem man die Aufteilung in Merkmale und Zielvariable festlegt.
6-3 Aufteilung in Trainings- und Testdaten
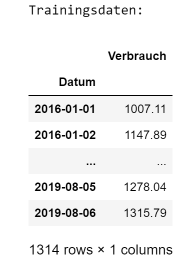
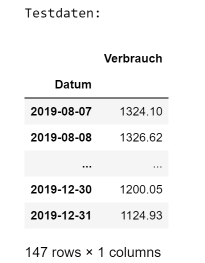
Die Verbrauchsdaten, die in dem einspaltigen DataFrame series gespeichert sind, werden nun entsprechend dem Modells des Überwachten Lernens in Trainings- und Testdaten aufgeteilt. Hier verwenden wir die Pandas-Funktion iloc, um die neuen DataFrames train und test zu extrahieren. Mit Hilfe der Trainingsdaten train wird das neuronale Netzwerk erstellt und mit Hilfe der Testdaten test wird es validiert. Der Anteil der Trainingsdaten, die für Validierung verwendet werden, wird durch den Konfigurationsparameter VALIDATION_SPLIT gesteuert. Wir verwenden 90% der Daten für das Training und 10% für die Validierung, weitere getestete Aufteilungen waren 80%-20%.
Codezelle 6: Aufteilung in Trainings- und TestdatenAusgabe:VALIDATION_SPLIT = 0.1train_size = int(len(series) * (1-VALIDATION_SPLIT))test_size = len(series) - train_sizetrain = series.iloc[0:train_size,:]test = series.iloc[train_size:len(series)]print("Trainingsdaten:")display_dataframe(train, 4)print("Testdaten:")display_dataframe(test, 4)
6-4 Skalierung der Daten
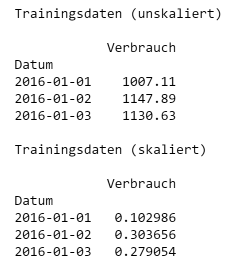
Die Eingabedaten eines Neuronalen Netzwerkes müssen vor der Trainingsphase skaliert werden, um zur Größenordnung der Gewichte zu passen und und somit einen stabil verlaufenden Trainingsprozess zu ermöglichen. Beim Trainieren eines Neuronalen Netzes mit Keras können die Eingabedaten mit Hilfe der Methode fit_transform() der Klasse MinMaxScaler in den Wertebereich (0, 1) skaliert werden. Die Funktion erwartet eine Eingabe der Form "n Beobachtungen, n Merkmale" und gibt ein NumPy ndarray mit skalierten Werten zurück. D.h. unsere Trainingsdaten train mit 1314 Beobachtungen und 1 Merkmal werden als Eingabe akzeptiert, als Rückgabewert erhalten wir ein NumPy-Array train_s. Für die Veranschaulichung / Ausgabe wird hier aus dem NumPy-Array noch ein DataFrame dftrain_s erstellt, das mit dem passenden Datum-Bereich als Index versehen wird.
Zur Kontrolle geben wir die ersten drei Zeilen der Trainingsdaten vor und nach der Skalierung aus.
| Codezelle 7: Skalierung | Ausgabe: train, dftrain_s |
|---|---|
|
 |
6-5 Festlegen der Merkmale und Zielvariablen
Für die Prognose von Zeitreihen-Daten muss das Neuronale Netzwerk als ein Modell des überwachten Lernens formuliert werden.
Beim überwachten Lernen liegt für jeden Datensatz der Input-Daten (X) eine bekannte Bewertung (Y) vor, d.h. die Daten sind schon in Kategorien unterteilt.
Die Datenpunkte einer Zeitreihe müssen folglich aufgeteilt werden in Input-Daten (Merkmale, mit X bezeichnet) und eine Zielvariable (Y), die die Bewertung
der Merkmale enthält.
Wir erreichen die Aufteilung mit Hilfe der Funktion erzeuge_bewertung(data, timesteps), die für eine gegebene Zeitreihe
data und eine Anzahl von Schritten timesteps zwei Numpy-Arrays X und Y erstellt, die die Merkmale und Zielvariable enthalten.
Konkret werden aus der Zeitreihe z.B. timesteps = 7 Werte als Merkmale festgehalten, und der vierte Wert ist die Zielvariable,
für die die Bewertung schon bekannt ist.
Um die Funktion zu testen, werden die ersten 14 Zeilen der Spalte Verbrauch in ein DataFrame data extrahiert. Für das Array data werden anschließend mit Hilfe der Funktion erzeuge_bewertung() die Merkmale X und die Zielvariable Y extrahiert. Die Ausgabe zeigt zwei Numpy-Arrays: ein Array X mit 7 Zeilen und 7 Spalten und ein Array Y mit 7 Elementen. Die erste rot markierte Zeile von X stellt eine Gruppe von 7 Merkmalswerten dar, die durch den ersten Wert in Y (blau markiert) bewertet wird. Man beachte, dass bei diesem Vorgehen für die ersten sieben Zeilen des Datensatzes keine Bewertung vorliegt, da die entsprechenden Vergangenheitsdaten fehlen.
| Codezelle 8: Hilfsfunktion erzeuge_bewertung | Ausgabe: data, X, Y |
|---|---|
|
 |
Nachdem die Funktionsweise der Funktion erzeuge_bewertung() getestet wurde, wird sie auf die Trainings- und Testdaten angewendet. Die Funktion liefert als Rückgabewert aus den Trainingsdaten die Numpy-Arrays X_Train und Y_Train und aus den Testdaten die Numpy-Arrays X_Test und Y_Test. In Zeilen 6 bis 10 werden die Dimensionen der erzeugten Arrays zur Kontrolle ausgegeben.
Codezelle 9: Zielvariable extrahierenAusgabe:# X = Merkmale, Y = ZielvariableTIMESTEPS = 7X_Train, Y_Train = erzeuge_bewertung(train_s, TIMESTEPS)X_Test, Y_Test = erzeuge_bewertung(test_s, TIMESTEPS)print("Trainingsdaten:")print("X_Train: Zeilen {}, Spalten {}".format(*X_Train.shape))print("Y_Train: Zeilen {}".format(*Y_Train.shape))print("Testdaten:")print("X_Test: Zeilen {}, Spalten {}".format(*X_Test.shape))print("Y_Test: Zeilen {}".format(*Y_Test.shape))
Trainingsdaten: X_Train: Zeilen 1307, Spalten 7 Y_Train: Zeilen 1307 Testdaten: X_Test: Zeilen 140, Spalten 7 Y_Test: Zeilen 140
7 Modell erstellen und trainieren
Ein Modell wird erstellt, indem seine Netzwerk-Topologie festgelegt wird, d.h. die Anzahl, Art und Anordnung der Schichten, und die Verlustfunktion angegeben wird, die für das Ermitteln der optimalen Gewichtswerte verwendet werden soll. Die Verlustfunktion misst, wie gut die Ausgabe Y_Train_Pred des Modells für bestimmte Input-Daten X_Train mit der Zielausgabe Y_Train übereinstimmt. Ein Modell wird trainiert, indem unter Verwendung eines Optimierungsalgorithmus der Wert der Verlustfunktion während der Trainingsphase minimiert wird.
Die Keras-Bibliothek bietet zum Erstellen eines neuronalen Netzwerks zwei Klassen: Sequential und Functional, die beide die Erstellung mehrschichtiger Netzwerke unterstützen. Die Sequential-Klasse ermöglicht das sequentielle Zusammenzufügen von Schichten (engl. layer), während mit Hilfe der Functional-Klasse komplexere Anordnungen von Schichten erstellt werden können.
Die Schichten eines Künstlichen Neuronalen Netzwerks sind in Keras durch die Klassen der Layer-API realisiert: Conv2D, MaxPooling2D, Flatten, Dense, LSTM etc. Jede Layer-Klasse hat eine Gewichtsmatrix, eine Größenangabe für die Anzahl verwendeter Neuronen (units), eine Formatbeschreibung der Eingabedaten (input_shape), eine Aktivierungsfunktion (activation), und eine Reihe weiterer Parameter, die die Gestaltung der Schicht steuern.
Die üblichen Schritte beim Erstellen eines Neuronalen Netzwerks (Modell erstellen, Modell trainieren, Modell validieren und verwenden) werden in Keras mit Hilfe der Funktionen compile(), fit() und predict() durchgeführt.
7-1 Modell erstellen
Ein Modell wird erstellt, indem seine Netz-Topologie spezifiziert wird, d.h. die Anzahl der Bausteine (UNITS) und Schichten (LAYER) sowie deren Anordnung. Als Prognosemodell wird hier ein neuronales Netzwerk mit einer Eingabeschicht, einer Ausgabeschicht und fünf versteckten LSTM-Schichten erstellt.
- Zeile 1-4: Die Konfigurationsparameter für die Erstellung des Modells werden festgelegt.
- Zeile 5: Erstelle neues Sequential-Modell und lege seinen Namen fest.
- Zeile 7-12: Füge dem Modell in einer for-Schleife N_LAYER versteckte LSTM-Schichten hinzu. Für jede LSTM-Schicht wird die Anzahl der Ausgangsknoten festgelegt (UNITS) sowie das Format der Eingabedaten (input_shape). Weitere wichtige Parameter sind die Aktivierungsfunktion (activation), die für LSTM-Ausgabe defaultmäßig auf die sigmoid-Funktion festgelegt ist, und der dropout-Parameter, der festlegt, welcher Anteil an Ausgangsknoten der Schicht beim Trainieren "vergessen" werden soll.
- Zeile 9: Jede Zelle einer LSTM-Schicht erwartet eine dreidimensionale Eingabe. Eine LSTM-Schicht, die eine Eingabesequenz von Zeitreihendaten verarbeitet, wird jedoch einen einzelnen Wert als 2D-Array zurückliefern. Um mehrere LSTM-Schichten nacheinander schalten zu können, müssen wir daher die inneren LSTM-Schichten so konfigurieren, dass sie ein dreidimensionales Array ausgeben, welches als Eingabe vom nächsten LSTM-Layer verwendet werden kann. Die geschieht mit Hilfe des Parameters return_sequences = True
- Zeile 13: Als letzte Schicht fügen wir eine Dense-Schicht hinzu. Eine Dense-Schicht ist die Implementierung einer Standardschicht eines neuronalen Netzwerkes. Standardmäßig wird keine Aktivierungsfunktion verwendet, d.h. die Daten werden unverändert weitergegeben.
- Zeile 15: Die Methode compile() konfiguriert das Modell, d.h. bereitet es mit Hilfe der angegebenen Konfigurationsparameter für die Trainingsphase vor. Insbesondere kann hier eingestellt werden, welcher Optimierer und welche Metriken verwendet werden sollen. Mit Hilfe des Parameters loss wird konfiguriert, welche Performance-Metrik während des Trainings minimiert werden soll. Hier wird die mittlere quadratische Abweichung (mse) verwendet.
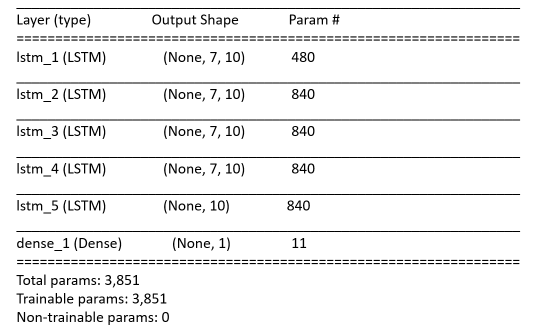
- Zeile 17: Die Zusammenfassung des Modells (vgl. Ausgabe 1) wird ausgegeben.
- Zeile 18: Visualisierung des Modells mit Hilfe der Funktion plot_model(), vgl. Ausgabe 2.
# KonfigurationsparameterTIMESTEPS = 7 # Länge eines gleitenden ZeitfenstersUNITS = 10 # Anzahl von Ausgängen bei einer LSTM-SchichtN_LAYER = 4 # Anzahl LSTM-Schichtenmodel = Sequential(name='sequential') # Erstelle ein sequentielles Modell# Füge Schichten hinzufor i in range(N_LAYER):lstm_layer = LSTM(units = UNITS, input_shape=(TIMESTEPS,1),return_sequences=True,name = 'lstm_' + str(i+1))model.add(lstm_layer)model.add(LSTM(units = UNITS, input_shape=(TIMESTEPS,1), name = 'lstm_' + str(N_LAYER+1)))model.add(Dense(units = 1, name='dense_1'))# Konfiguriere das Modell für die Trainingsphasemodel.compile(optimizer = "adam", loss = "mse", metrics=['mean_squared_error'])# Zusammenfassung und Visualisierung des Modellsmodel.summary()plot_model(model, show_shapes=True, show_layer_names=True)
Ausgabe: Visualisierung der Netzwerktopologie
| Ausgabe 1: | Ausgabe 2: |
|---|---|
 |
|
7-2 Modell trainieren
Das Trainieren des Modells geschieht mit Hilfe der Funktion fit(). Die Funktion erhält als Parameter die Merkmale und Zielvariable des Trainingsdatensatzes (X_Train und Y_Train) und trainiert daran in einer festgelegten Anzahl von Iterationen ("Epochen") das Neuronale Netzwerk, d.h. erlernt seine Gewichte. Der Rückgabewert der Funktion ist ein history-Objekt, das die beim Training ermittelten Performancemetriken speichert. Wichtige Konfigurationsparameter der Funktion sind:
- epochs: Anzahl der Epochen, d.h. Trainingsdurchläufen des Algorithmus. Da im Vornherein die erforderliche Anzahl an Epochen nicht bekannt ist, setzen wir diesen Parameter auf eine große Zahl und legen zusätzlich ein Stop-Kriterium über eine Callback-Funktion fest.
- batch_size: Größe eines Batchs. Ein Batch ist die Anzahl der Trainings-Beobachtungen (Zeilen), die der Algorithmus auf einmal bearbeitet. Bei einer Anzahl von 1000 Trainingsbeobachtungen und N_BATCH = 64wird das Netzwerk zunächst mit den ersten 64 Datensätzen trainiert, danach mit den nächsten 64 etc. Der Default-Wert für den Parameter batch_size ist 64.
- validation_split: Anteil der Trainingsdaten, die für die Validierung verwendet werden. Falls validation_split = 0.1 gesetzt wird, verwendet der Algorithmus die letzten 10% der Trainingsdaten für die Validierung.
- verbose: ein Parameter, der steuert, ob und wie Zwischenergebnisse des Trainings ausgegeben werden.
Für eine fortgeschrittenere Steuerung des Trainings verwenden wir zwei Callback-Funktionen:
- EarlyStopping: Die hier konfigurierte Callback-Funktion bewirkt, dass der Trainingsprozess gestoppt wird, wenn die Mittlere Quadratische Abweichung des Validierungsdatensatzes zu steigen beginnt, jedoch erst nach einer Wartezeit von 200 Epochen. Das zusätzliche Stopp-Kriterium ist wichtig, da ein optimales Modell dann erreicht wird, wenn das Trainings-Performancemaß ein Plateau erreicht hat,und das Validierungs-Performancemaß gerade wieder anfängt zu steigen. Eine zu lange Trainingsphase würde zu keiner Verbesserung mehr führen und die laufzeit unnötig verlängern.
- CSVLogger: Mit Hilfe des CSVLogger-Callbacks kann die Ausgabe des Trainingsprozesses in die angegebene extrene Log-Datei gespeichert werden.
Das trainierte Modell kann in verschiedenen Formaten (JSON oder HDF5) für die spätere Verwendung gespeichert werden.
Codezelle 11: Modell trainierenAusgabe:# Erstelle Callback für Stop-Kriteriumfrom keras.callbacks import EarlyStopping, CSVLoggercb_stop = EarlyStopping(monitor='val_loss', mode='min',verbose=1, patience=200)log_file = 'demo-py5-log.csv'cb_logger = CSVLogger(log_file, append=False, separator=';')# X_Train erhält eine zusätzliche DimensionX_Train = np.reshape(X_Train,(X_Train.shape[0], X_Train.shape[1], 1))# Trainiere das Modell mit Hilfe der Funktion fit()BATCH_SIZE = 64history = model.fit(X_Train, Y_Train,epochs=EPOCHS, batch_size=BATCH_SIZE,validation_split=VALIDATION_SPLIT, verbose=2,callbacks=[cb_logger, cb_stop])# Speichere das Modell im Format HDF5model.save("model_adam.h5")print("History");print(history.history.keys());

Falls der Parameter verbose den Wert 2 erhält, sieht eine Ausgabe des Training-Prozesses ähnlich wie abgebildet aus. Für jede Epoche wird eine Zeile mit der benötigten Zeit und den Werten der Performance-Metriken angezeigt, die beim Training verwendet werden. Die Performance-Metriken 'loss' und 'mean_squared_error' beziehen sich auf die Trainingsdaten, die Performance-Metriken 'val_loss' und 'val_mean_squared_error' hingegen auf die Validierungsdaten. Bei einem gut verlaufenden Training sollte die loss-Funktion der Trainingsdaten in ein Plateau führen, während die loss-Funktion der Validierungsdaten bis zu einem bestimmten Punkt fällt, dann aber wieder ansteigt.
7-3 Trainingsphase visualisieren
Die bei der Durchführungs des Trainings verwendeten Metriken können dem history-Objekt entnommen und grafisch dargestellt werden.
Mit history.history['mean_squared_error'] greift man auf die ermittelte mittlere quadratische Abweichung zurück, die
bei der Vorhersage auf den Trainingsdaten ermittelt wird, und mit history.history['val_mean_squared_error'] auf den MSE-Fehler,
der bei den Testdaten entsteht.
plt.plot(history.history['mean_squared_error'], label='MSE (Trainingsdaten)')plt.plot(history.history['val_mean_squared_error'], label='MSE (Testdaten)')plt.title('Training: Entwicklung des Fehlers')plt.ylabel('MSE-Fehler')plt.xlabel('Epochen')plt.legend()
Die Visualisierung der Trainingsphase zeigt, dass der MSE-Fehler in den Trainingsdaten kontinuierlich sinkt, schließlich ein stabiles Plateau erreicht und sich nicht mehr verbessert. Der MSE-Fehler der Testdaten fällt bis zu einer Epoche E1 gleichzeitig mit dem MSE der Trainingsdaten, und liegt wie erwartet leicht drüber. Bei einer späteren Epoche E2 wird der MSE der Testdaten wieder anfangen zu steigen, dann greift das Stopp-Kriterium und das Training wird beendet. Da die gängigen Implementierungen Künstlicher Neuronalen Netzwerke (hier: Tensorflow) nichtdeterministischen Trainingsalgorithmen verwenden, wird bei jedem Trainingsdurchlauf ein anderes Modell erstellt, und auch das Stoppkriterium greift einmal früher und einmal später.
Ausgabe: Trainings- vs. Validierungsfehler8 Modell validieren
Mit Hilfe des Testdatensatzes wird das Modell validiert, d.h. es wird eine Prognose erstellt und für diese werden Performancemetriken ausgewertet.
Bei der Validierung der Prognose-Ergebnisse sind die Mittlere Quadratische Abweichung (MSE) und deren Wurzel (RMSE), geeignete Performance-Maße, um die Güte einer Prognose zu bewerten. Die Mittlere Quadratische Abweichung ist der erwartete quadratische Abstand der Prognosewerte von den tatsächlichen Werten und wird berechnet, indem man die Differenzen der einzelnen absoluten Fehler quadriert und danach aufsummiert, dadurch wird die Auswirkung einzelner Abweichungen gemittelt. Die Wurzel RMSE aus der Mittleren Quadratischen Abweichung "bestraft" große Abweichungen und hat darüber hinaus dieselbe Maßeinheit wie die Zielvariable.
8-1 Prognose für Validierungsdaten
Zunächst erstellen wir eine Prognose für die skalierten Testdaten mit Hilfe der Methode predict() der Klasse Sequential. Die Funktion predict() erhält als Parameter den skalierten Testdatensatz X_Test und liefert die Prognose-Werte Y_Pred zurück. Die bekannten und geschätzten Werte der Zielvariablen (Y_Test und Y_Pred) werden anschließend in ihren ursprünglichen Wertebereich reskaliert.
- Zeile 2-5: Die Testdaten X_Test und Y_Test erhalten eine zusätzliche Dimension, um als Eingabeparameter der Funktionen predict() bzw. inverse_transform() akzeptiert zu werden. D.h. X_Test wird ein dreidimensionales Array und Y_Test ein zweidimensionales Array.
- Zeile 6: Die predict-Funktion liefert die geschätzten Werte der Zielvariablen y_Pred zurück.
- Zeile 7-11: Die tatsächlichen und geschätzten Werte der Zielvariablen werden mit Hilfe der Funktion inverse_transform in den ursprünglichen Wertebereich reskaliert.
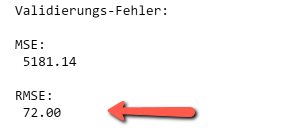
- Zeile 12-17: Berechnung und Ausgabe von MSE und RMSE.
| Codezelle 13: Validierung | Ausgabe: |
|---|---|
|
|
8-2 Performance der Validierung ermitteln
Nachdem die Vorhersagewerte für die Testdaten ermitteln wurden, berechnen wir noch die maximale Abweichung zwischen tatsächlichen und geschätzten Testdaten und visualisieren diese. Dafür wird ein neuer DataFrame pred durch Zusammenfügen der DataFrames y_Test, y_Pred erstellt, dem wir noch zwei weitere Spalten hinzufügen, die den absoluten und den relativen Fehler enthalten.
Um den Code übersichtlicher zu halten, schreiben wir eine Hilfsfunktion rel_error(df, col1, col2), die für ein DataFrame df und zwei namentlich gegebene Spalten col1 und col2 den relativen Fehler der Spalten berechnet und in einer neuen Spalte mit dem Namen Error (%) speichert.
def rel_error(df, col1, col2):df['Error (%)'] = (df[col1] - df[col2]) / df[col1] * 100df['Error (%)'] = df['Error (%)'].abs()return df['Error (%)']
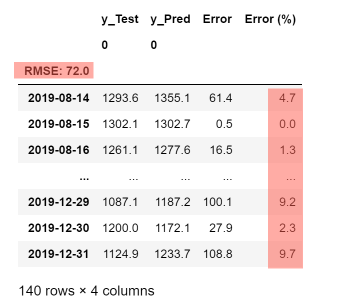
Der folgende Codeblock fügt die DataFrames y_Test und y_Pred mit Hilfe der Funktion concat() zu einem neuen DataFrame mit dem Namen pred zusammen. Das Zusammenfügen geschieht entlang der Spalten, was durch die Angabe axis=1 festgelegt wird. Der neue DataFrame erhält das Datum als Index-Spalte sowie zwei neuen Spalten, die den absoluten und den relativen Fehler der ersten beiden Spalten enthalten. Der RMSE-Wert 75 ist so zu interpretieren, dass die Abweichung der Prognose im Mittel um 75 GwH von den tatsächlichen Werten abweicht, dies beträgt 6% vom Mittelwert der Verbrauchsdaten und ist ein akzeptables Ergebnis. Den punktweisen relativen Fehler haben wir zusätzlich ermittelt, um die Stellen mit den maximalen Abweichungen herauszufinden. Diese liegen mit max. 20% wie erwartet um die Jahreswende.
Codezelle 14: FehleranalyseAusgabe:# Hilfsfunktion error_table erzeugt Fehlertabelledef error_table(df1, df2, col1, col2, idx):cols = [df1, df2]headers = [col1, col2]# Erzeuge pred aus y_Test und y_Pred mit Index idxpred = pd. concat(cols, axis=1, keys=headers)pred.set_index(idx, inplace=True)# Füge Fehler-Spalten hinzupred['Error'] = np.abs(pred['y_Test'] - pred['y_Pred'])pred['Error (%)'] = rel_error(pred, 'y_Test', 'y_Pred')pred = pred.astype(float).round(1)# Füge RMSE hinzumse = mean_squared_error(df1, df2)rmse = np.round(np.sqrt(mse))pred.index.name = "RMSE: " + str(rmse)return pred# Erzeuge Fehlertabelle für Validierung und gebe sie ausidx = test.index[TIMESTEPS:anzZ];pred = error_table(y_Test, y_Pred, 'y_Test', 'y_Pred', idx)display_dataframe(pred)
8-3 Prognose für Validierung visualisieren
Die Prognose für die Testdaten, wie sie im DataFrame pred enthalten ist, wird nun visualisiert. Die Funktion plot_prediction(pred) enthält den Visualisierungscode, hier wird ein Diagramm erstellt, das die ersten zwei Spalten eines DateFrames pred plottet, das Diagramm mit Beschriftungen versieht und als SVG-Datei speichert.
- Zeile 2: Erstelle Figur mit zwei Diagrammen, die nebeneinander angeordnet sein sollen, und gebe die Größe der Figur an.
- Zeile 3-9: Zeichne die erste und zweite Spalte des DataFrames pred auf das erste Diagramm.
- Zeile 11-15: Zeichne den relativen Fehler auf das zweite Diagramm.
def plot_prediction(pred, file):sns.set(rc={'figure.figsize':(10, 5)})sns.set_color_codes('bright')ax = pred.iloc[:,0].plot(label='Verbrauch', linewidth=1, color='b');ax = pred.iloc[:,1].plot(label='Verbrauch (geschätzt)',linewidth=1, color='g', linestyle='dashed', marker='o');ax.set_title('Stromverbrauch: Tatsächliche vs. geschätzte Daten')ax.set_ylabel('GwH');ax.legend();plt.savefig(file, dpi=400, bbox_inches='tight')plot_prediction(pred, 'juno_out_pred.svg')
Das Diagramm zeigt den tatsächlichen vs. den geschätzten Verbrauch. Der RMSE-Fehler ist in einem akzeptablen Bereich, der punkteweise relative Fehler liegt in einigen Bereichen (speziell Jahreswende) jedoch um bis zu 30% falsch, was auf die nicht behandelte Saisonalität zurückzuführen ist.
Ausgabe9 Prognose für 2020
In diesem Schritt wird das zuvor erstellte Neuronale Netzwerk eingesetzt, um eine Prognose für das Jahr 2020 zu erstellen. Für die Prognose mit neuen Testdatensätzen kann der Code aus Abschnitt "Modell validieren" wiederverwendet werden. Es bietet sich an, aus den Codefragmenten für die Vorhersage eine wiederverwendbare Funktionen zu extrahieren: Die Funktion prognose(df, colname) erstellt eine Prognose für die Spalte colname des DataFrames df und liefert einen DataFrame pred zurück, der tatsächliche und geschätzte Werte sowie zwei Fehlerspalten enthält.
Codezelle 16: Hilfsfunktion prediction# Funktion erstellt eine Prognose für die Spalte colname des DataFrames df# df: DataFrame# colname: Spalte des DataFrames, für die die Prognose erstellt werden soll.# pred: Rückgabewert: ein DataFrame mit 4 Spalten: y_Test, y_Pred, Error, Error %def prognose(df, colname):anzZ = df.shape[0] # Anzahl Zeilenseries = df[colname] # Spalte# Skaliere auf (0, 1)test = scaler.fit_transform(series.values.reshape(anzZ, 1))# Erzeuge BewertungX_Test, Y_Test = erzeuge_bewertung(test, TIMESTEPS)# Zusätzliche DimensionenX_Test = np.reshape(X_Test, (X_Test.shape[0], X_Test.shape[1], 1))Y_Test = np.reshape(Y_Test, (Y_Test.shape[0], 1))# Erstelle PrognoseY_Pred = model.predict(X_Test)# Reskaliere die Dateny_Test = pd.DataFrame(scaler.inverse_transform(Y_Test))y_Pred = pd.DataFrame(scaler.inverse_transform(Y_Pred))# Tabelle für Ausgabeidx = series.index[TIMESTEPS:]pred = error_table(y_Test, y_Pred, 'y_Test', 'y_Pred', idx)return pred
Die Prognose erfolgt nun in fünf Schritten: Einlesen der Testdaten in einen DataFrame opsd_test, Erstellen der Prognose mit Hilfe eines Funktionsaufrufs der Funktion opsd_prediction(), Ausgabe des DataFrames, Berechnung der Performance-Metriken und visuelle Darstellung der geschätzen Werte und des Fehlers.
Codezelle 17: Prognose für 2020Ausgabe:# (1) Testdaten einlesenopsd_test = pd.read_csv( 'https://www.elab2go.de/demo-py5/opsd_2020.csv')opsd_test.set_index('Datum', inplace = True)opsd_test.loc[:,:].fillna( method='pad', inplace = True)opsd_test = opsd_test.astype(float).round(2)# (2) Erstelle Vorhersage mit Funktion opsd_predictionpred_test = opsd_prediction(opsd_test, 'Verbrauch')# (3) Gebe pred_test ausdisplay_dataframe(pred_test, 6)# (4) Berechne Performance-Metrikenperf_prediction(pred_test)# (5) Visualisiere Prognose für 2020plot_prediction(pred_test)
Performance-Metriken und Visualisierung zeigen eine akzeptable Prognose, mit einem RMSE-Fehler von 75 der wie erwartet größer ist als der in den Validierungsdaten.
10 Zusammenfassung und Ausblick
Demo-PY5 zeigt, wie ein Neuronales Netzwerk mit mehreren LSTM-Schichten für die Zeitreihenprognose mit Hilfe der Python-Bibliotheken Keras und Tensorflow erstellt wird. Die Trainingsaufgabe besteht darin, in einem rollenden Zeitfenster aus TIMESTEPS bekannten Werten einen Zukunftswert zu schätzen. Für die Bewertung des Modells verwenden wir die mittlere quadratische Abweichung als Performance-Maß. Die Güte des Modells beruht auf der richtigen Konfiguration des Netzes (Anzahl an LSTM-Schichten und Neuronen) und der Einstellung der Konfigurationsparameter für die Trainingsphase, insbesondere die beste Anzahl der Epochen für ein gutes Modell, das weder unter- noch überangepasst ist.
Die vorliegende Version der Demo-PY5 ersetzt eine ältere erste Version Demo-PY5 2018, die die Zeitreihenanalyse auf einem Datensatz über die Jahre 2014 bis 2018 durchgeführt hat.
Jupyter Notebook (Google Colab)
Die Schritte des Überwachten Lernens, die die Erstellung und Verwendung eines Neuronalen Netzwerks für die Prognose von Stromverbrauchsdaten veranschaulichen, sind in einem Jupyter Notebook abgebildet, das in Google Colab abgelegt ist und von dort bezogen werden kann.
YouTube-Video
Die Verwendung des erstellten Jupyter Notebook zur ersten Version wird durch ein Video (Screencast mit zusätzlichen Erläuterungen) veranschaulicht.
Autoren, Tools und Quellen
Autor:
Prof. Dr. Eva Maria Kiss
Mit Beiträgen von:
B. Sc. Franc Willy Pouhela
M. Sc. Anke Welz
Tools:
Keras, Pandas,
Tensorflow,
Python, Jupyter Notebook
Quellen und weiterführende Links:
- Hochreiter, Sepp & Schmidhuber, Jürgen. (1997). Long Short-term Memory. Neural computation. 9. 1735-80.
- McKinney, Wes (2019): Datenanalyse mit Python. Auswertung von Daten mit Pandas, NumPy und IPython. 2. Auflage. Heidelberg: O'Reilly.
- Pouhela, Franc. (2020). Bachelorarbeit: Datenanalyse und Vorhersage mit Python und Keras für Open Power System-Daten.
- Russell, Stuart J., Norvig, Peter (2014) Artificial intelligence. A modern approach.
- Python-Tutorial: https://www.elab2go.de/demo-py1/
- Jupyter Notebooks verwenden: https://www.elab2go.de/demo-py1/jupyter-notebooks.php
- Jupyter Notebook Widgets erstellen: https://www.elab2go.de/demo-py1/jupyter-notebook-widgets.php
- Interaktive Datenvisualisierung in Python: https://www.elab2go.de/demo-py2/